I. Prérequis▲
Les prérequis techniques sont identiques au premier épisode disponible ici.
Pour ce deuxième épisode, nous allons partir du projet issu du premier. Vous pouvez donc au choix :
- reprendre directement votre projet issu de l’épisode 1 ;
- faire une copie du projet de l’épisode 1 dans un nouveau répertoire dédié à l’épisode 2. Vous conserverez ainsi une version du projet pour chaque étape.
Quel que soit votre choix, ouvrez Delphi et chargez votre projet.
II. Déplacement▲
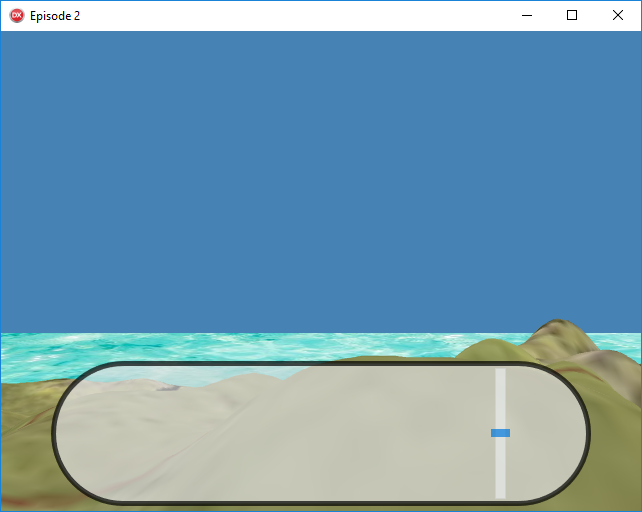
À l’issue de l’épisode 1, nous avons généré une île en 3D, entourée d’une mer, puis nous avons agrémenté le tout en appliquant des textures et une animation.
Nous allons maintenant permettre à l’utilisateur de se déplacer dans ce décor en vue subjective. L’utilisateur va donc pouvoir interagir en faisant bouger le point de vue (la caméra).
Toutefois, dans cet épisode, nous n’aborderons ni la détection et la collision des objets, ni une quelconque forme de physique (frottements, gravité…). L’utilisateur pourra se déplacer si librement qu’il passera à travers le décor !
La première chose que nous allons faire est de supprimer l’animation (le TFloatAnimation). En effet, elle était présente uniquement pour avoir une meilleure vision de l’île en la faisant tourner automatiquement autour de son axe Y.
Ensuite, pour gérer un déplacement, il nous faut combiner deux choses : une vitesse et une orientation. Nous allons commencer par gérer la vitesse, car il s’agit de la partie la plus simple. L’orientation sera traitée dans le chapitre suivant.
La vitesse va être une simple valeur numérique qui provoquera :
- un déplacement vers l’avant lorsqu’elle sera positive ;
- un déplacement vers l’arrière lorsqu’elle sera négative ;
- l’arrêt lorsqu’elle sera nulle.
Afin que l’utilisateur puisse doser à sa guise la vitesse, nous allons utiliser un TTrackBar. Mais, avant de placer ce composant sur la fiche, et comme il s’agit du premier composant d’interaction homme/machine, nous allons préparer une zone en bas de l’écran qui accueillera également les futurs composants visuels.
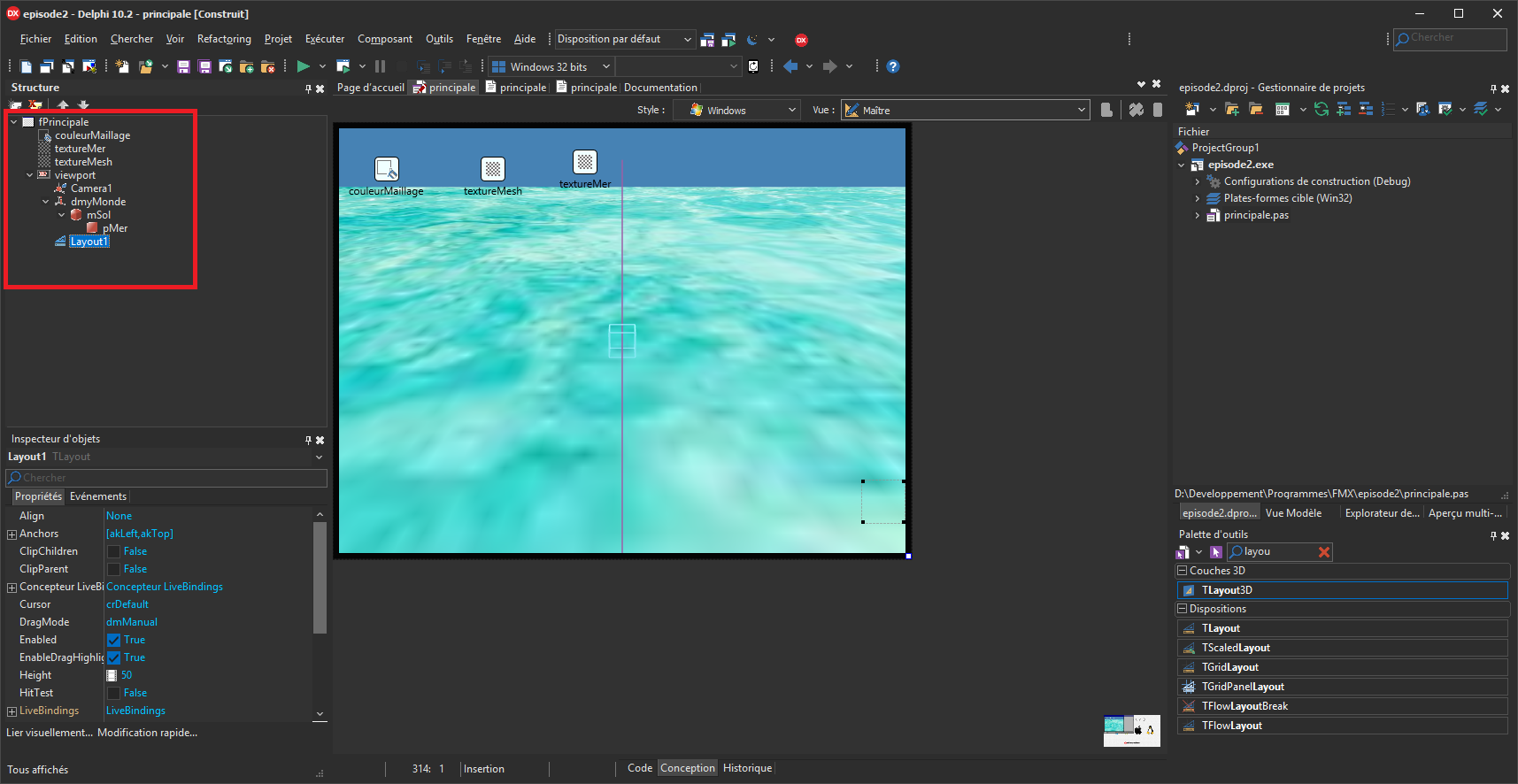
Plaçons tout d’abord un TLayout (rubrique « Dispositions ») sur la fiche et via la vue Structure, plaçons-la en tant qu’enfant du Viewport.
Via l’inspecteur d’objets, modifions ses propriétés :
- Align à Bottom ;
- Height à 150;
- Name à layIHM.
Ensuite, plaçons un TRoundRect (rubrique « Formes ») en tant qu’enfant de layIHM et modifions ses propriétés :
- Align à Client ;
- Margins aux valeurs : Bottom 5, Left 50 et Right 50;
- Opacity à 0,7;
-
Stroke avec une valeur Thickness à 5.
Plaçons un nouveau TLayout en tant qu’enfant du TRoundRect que nous configurons via l’inspecteur d’objets de la manière suivante :
-
Align à Right ;
-
Margins aux valeurs : Bottom 5, Left 2, Right 50 et Top 5 ;
-
Name à layVitesse.
Enfin, plaçons le TTrackBar (rubrique « Standard ») en tant qu’enfant du layVitesse et via l’inspecteur d’objets, affectons-lui les valeurs suivantes :
-
Align à Client ;
-
Frequency à 0,1;
-
Margins aux valeurs : Bottom 2 et Top 2;
-
Orientation à vertical ;
-
Max à 8 ;
-
Min à -8 ;
- Name à tbVitesse.
Le fait de jouer avec les TLayout et les propriétés Align des composants permet à l’interface de s’adapter automatiquement aux redimensionnements de la fenêtre.
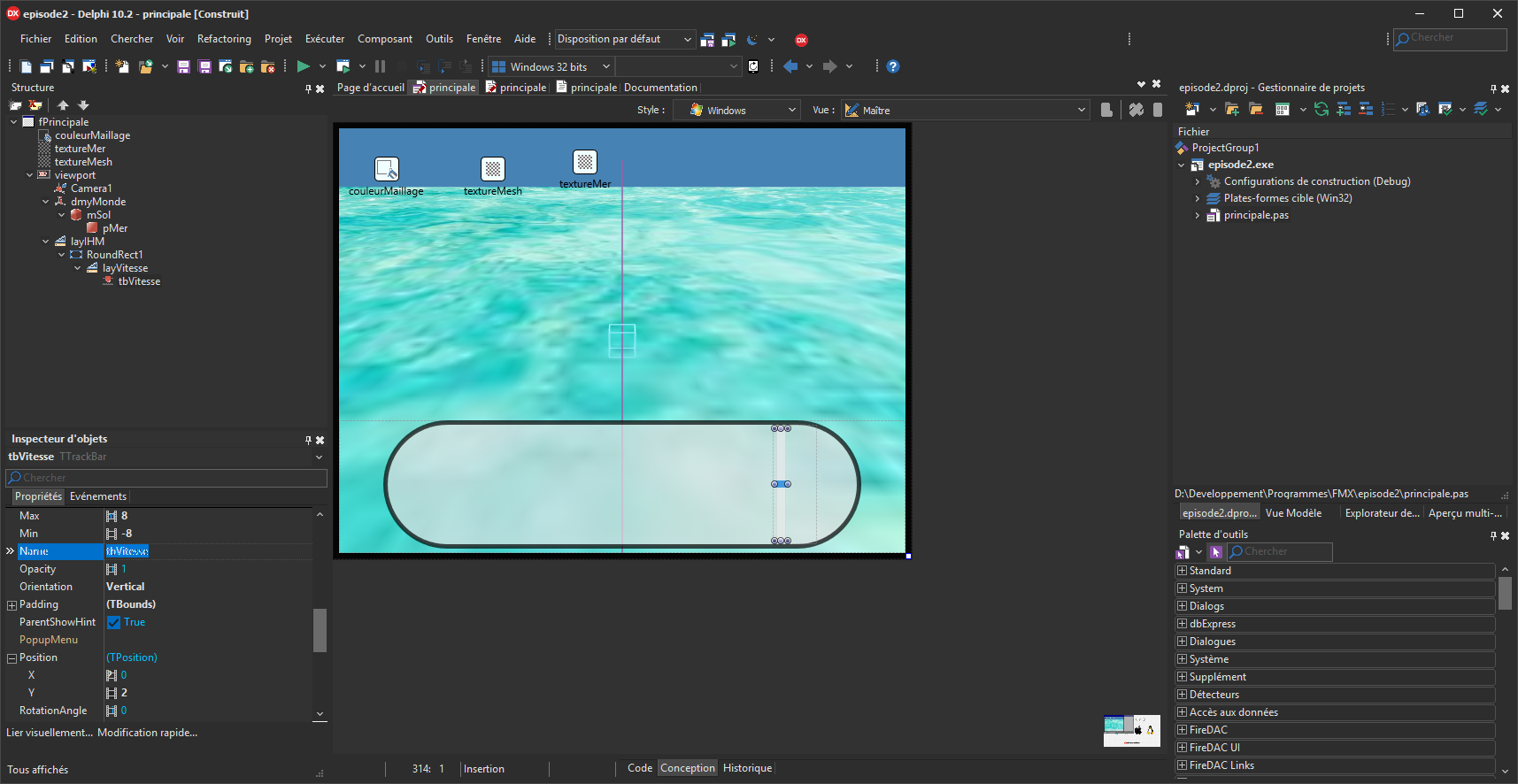
À ce stade, vous devez obtenir ceci :
Il nous reste maintenant à prendre en compte la valeur du tbVitesse pour déplacer la caméra. Pour ce faire, générons l’événement OnChange du tbVitesse via l’inspecteur d’objets et entrons le code suivant :
procedure TfPrincipale.tbVitesseChange(Sender: TObject);
begin
Camera1.Position.Z := Camera1.Position.Z - tbVitesse.Value;
end;Nous y déplaçons simplement la caméra sur l’axe Z (la profondeur) en fonction de la valeur du tbVitesse. Attention : comme nous souhaitions qu’une valeur positive de la vitesse fasse avancer le point de vue et que l’axe Z est orienté dans le sens inverse (les valeurs positives vers l’arrière), il faut bien faire une soustraction.
En l’état, si vous exécutez le projet, vous constaterez que le point de vue devient mobile en fonction de la valeur du tbVitesse.
Nous nous déplaçons pour le moment uniquement vers l’avant ou l’arrière. Nous verrons bientôt comment nous orienter. Patience !
Nous allons améliorer le comportement du déplacement. En effet, nous ne nous déplaçons que lorsque nous changeons la valeur du tbVitesse et ce n’est pas tout à fait ce que nous souhaitons. Il serait mieux de continuer à nous déplacer à une vitesse constante (la valeur du tbVitesse) même lorsque nous n’agissons plus sur le TTrackBar.
Pour ce faire, nous allons utiliser un TFloatAnimation (rubrique « Animations ») qui fera office de boucle principale pour notre application. Si vous avez suivi mes autres tutoriels (le jeu de Pong en 3D ou FMX Corridor), vous remarquerez que c’est la technique que j’avais déjà employée pour ces deux jeux.
Choisissons donc un TFloatAnimation que nous placerons en tant qu’enfant de fPrincipale (directement, car il s’agit de la boucle principale) : elle ne sera pas liée à un objet 3D particulier.
Via l’inspecteur d’objets, modifiez ses propriétés de la manière suivante :
- Enabled à true ;
- Loop à true ;
- PropertyName à Tag ;
- StopValue à 1.
Cette animation sera ainsi infinie, car on lui indique de boucler (Loop à true) et que la fin surviendra lorsque sa propriété tag sera à 1, ce qui n’arrivera jamais.
Générons maintenant son événement OnProcess afin de spécifier les actions à réaliser pendant l’animation. Nous allons reprendre dans cet événement le code précédemment mis dans l’événement OnChange du tbVitesse. La reprise du code peut se faire par un couper-coller puisque nous n’aurons plus besoin de l’événement OnChange du tbVitesse.
À la place du OnChange du tbVitesse, nous avons maintenant le code :
procedure TfPrincipale.faniPrincipaleProcess(Sender: TObject);
begin
Camera1.Position.Z := Camera1.Position.Z - tbVitesse.Value;
end;Exécutons à nouveau le programme et nous remarquons que le comportement est à présent conforme à ce que nous souhaitions.
Pour terminer ce chapitre sur le déplacement, nous allons ajouter un petit bonus. Nous allons permettre à l’utilisateur d’utiliser la molette de la souris pour avancer ou reculer. Cela évitera à l’utilisateur de déplacer le pointeur de la souris sur le tbVitesse à chaque fois qu’il voudra modifier la vitesse.
Sélectionnons le Viewport et générons son événement OnMouseWheel. Cet événement se déclenche lorsque l’utilisateur agit sur la molette de la souris quel que soit le sens de rotation de la molette. Saisissons le code suivant dans l’événement généré :
procedure TfPrincipale.viewportMouseWheel(Sender: TObject; Shift: TShiftState; WheelDelta: Integer; var Handled: Boolean);
begin
tbVitesse.Value := tbVitesse.Value - (WheelDelta/400);
end;L’information WheelDelta est fournie en paramètre de l’événement : il s’agit du décalage de la molette. Nous utilisons donc ce paramètre afin de déterminer une nouvelle valeur au tbVitesse, ce qui aura pour effet de modifier la vitesse de déplacement dès la prochaine itération de faniPrincipale.
Vous pouvez exécuter à nouveau le projet et vous constaterez que vous pouvez maintenant avancer et reculer via la molette de la souris.
III. Orientation▲
La gestion du déplacement et de sa vitesse ne pose pas de problème particulier. Mais pour l’instant, nous ne nous déplaçons que sur l’axe Z (axe de profondeur). C’est bien, mais c’est tout de même très limité !
Dans ce chapitre, nous allons apprendre à nous orienter afin de donner une direction au déplacement.
III-A. La théorie▲
L’orientation s’effectuera à l’aide de la souris : l’utilisateur devra cliquer sur le TViewPort3D, puis, tout en maintenant le bouton gauche enfoncé, déplacer la souris.
Ce déplacement du pointeur de la souris va nous permettre d’obtenir l’orientation à donner à notre point de vue.
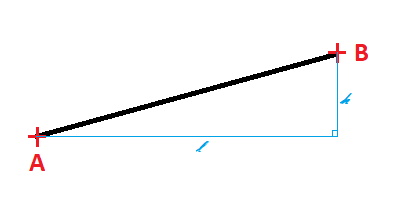
Grâce aux coordonnées de ces points, nous pouvons déterminer l (la distance entre les points A et B sur l’axe X) et h (la distance entre les points A et B sur l’axe Y).
Nous utiliserons les valeurs l et h pour orienter le point de vue de l’utilisateur de la manière suivante :
- l sera utilisée pour déterminer la rotation à effectuer du point de vue de l’utilisateur autour de l’axe Y (orientation droite/gauche) ;
- h sera utilisée pour déterminer la rotation à effectuer du point de vue de l’utilisateur autour de l’axe X (orientation haut/bas).
Voyons maintenant comment déterminer la rotation à appliquer en fonction des valeurs l et h.
En effet, nous allons gérer une certaine sensibilité entre le mouvement de la souris et les angles de rotation à appliquer au point de vue. Cette sensibilité est un rapport entre la largeur de la fenêtre principale et la valeur l et, de même, entre la hauteur de la fenêtre et la valeur h.
Dans notre projet, nous allons appliquer les règles suivantes :
- si l’utilisateur clique au milieu de l’écran puis qu’il déplace horizontalement le curseur de la souris jusqu’au bord droit de la fenêtre, nous devons faire tourner le point de vue vers la droite de 90° ;
- de même, si l’utilisateur clique au milieu de l’écran puis qu’il déplace verticalement le curseur de la souris jusqu’au bord haut de la fenêtre, nous devons faire tourner le point de vue vers le haut de 90°.
Illustration :
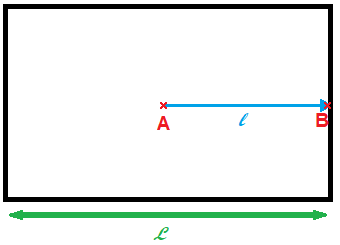
Comme précédemment, l représente le déplacement horizontal du pointeur de la souris en pixels. L représente la largeur de la fenêtre principale. Pour un déplacement horizontal de l pixels où l est la moitié de L, nous tournerons le point de vue vers la droite de 90°.
Pour un déplacement horizontal de L, nous ferons un demi-tour (rotation de 180°). Le rapport entre l et l’angle de rotation à effectuer autour de l’axe Y sera donc :
angleY = l * (180/ L)
Nous aurons un rapport similaire entre le déplacement en hauteur et l’angle de rotation à appliquer sur l’axe X :
angleX = h * (180/ H)
où h représente le déplacement vertical du pointeur de la souris et H la hauteur de la fenêtre principale.
Cette sensibilité est purement arbitraire, mais elle me paraît naturelle. En reprenant l’illustration précédente, vous pouvez choisir qu’en déplaçant le curseur de la souris sur la moitié de la largeur de l’écran, cela ne provoquera qu’une rotation de 45°. Cela signifiera que le rapport entre le déplacement de la souris et l’orientation du point de vue sera plus fin (un déplacement sur la largeur totale de la fenêtre provoquera une rotation de 90° au lieu de 180°), mais qu’il faudra s’y reprendre à deux fois avec la souris pour faire un demi-tour.
Jouer sur cette sensibilité pourrait servir par exemple pour modifier la résistance de l’environnement extérieur sur la mobilité du joueur. Ceci permettrait de forcer le joueur à fournir plus d’efforts (déplacer davantage la souris) pour se déplacer dans de l’eau que dans de l’air.
Nous venons de voir que l’orientation sera décomposée en deux temps avec un petit calcul supplémentaire en fonction de la sensibilité.
Le découpage en deux temps du mouvement d’orientation va nécessiter une astuce. En effet, si nous appliquons ces deux rotations à l’objet 3D de la caméra (le point de vue de l’utilisateur), nous n’obtiendrons pas le résultat escompté : la première rotation aura fait tourner le repère X,Y,Z : la valeur h à appliquer sur l’axe X ne sera plus bonne, car l’axe X aura également tourné.
Explications :
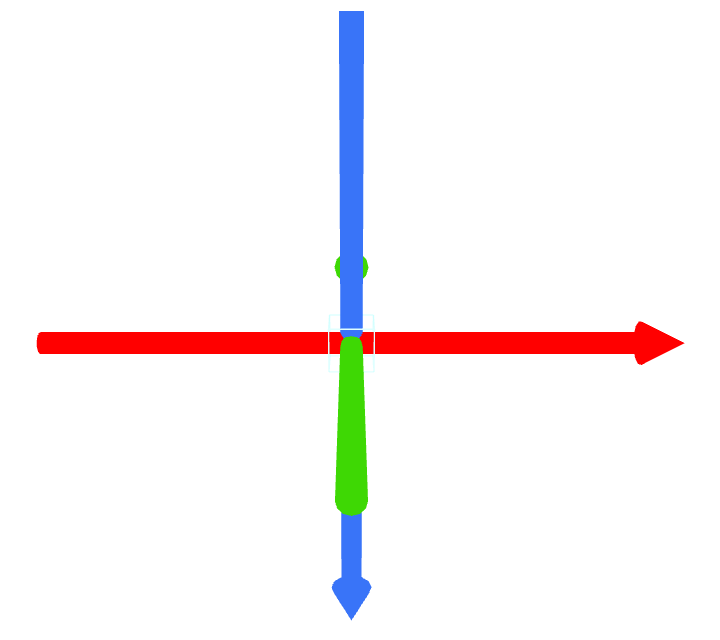
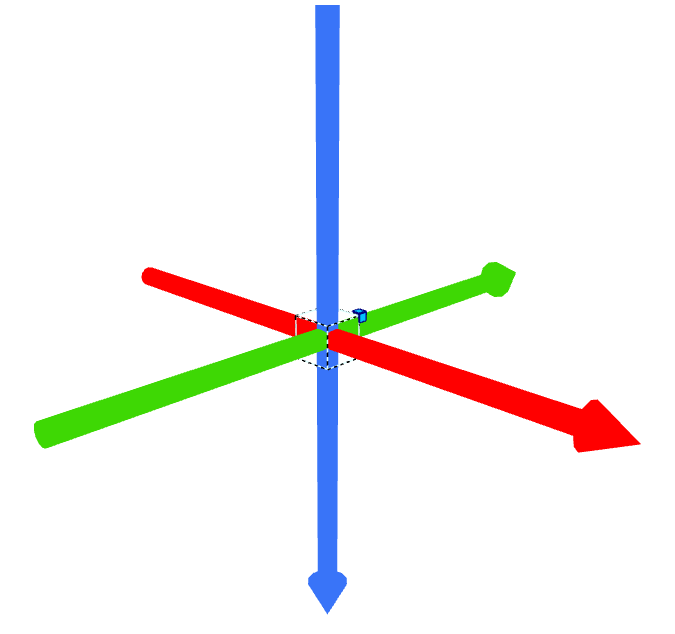
Voici notre repère X (en rouge), Y (en bleu), et Z (en vert).
Si nous lui appliquons une rotation de 45° autour de l’axe Y, le repère devient :
Nous constatons effectivement que l’axe X (en rouge) a tourné. Si nous appliquons telle quelle la valeur h à l’angle de rotation sur l’axe X, nous n’obtiendrons pas le résultat escompté : nous aurons l’impression que l’utilisateur penche la tête.
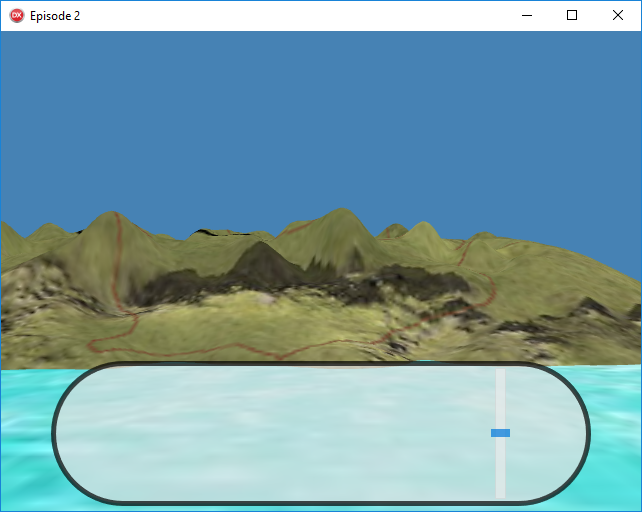
La vue d’origine :
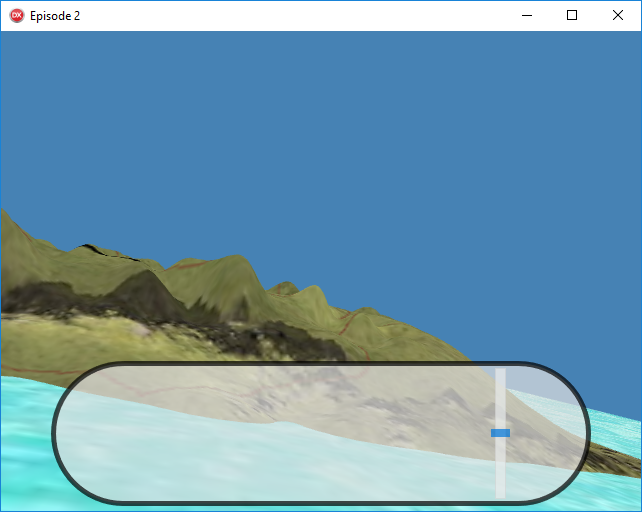
La vue obtenue en appliquant sur la caméra 10° de rotation sur l’axe X (propriété RotationAngle.X) et également 10° sur l’axe Y (propriété RotationAngle.Y) :
Pour notre projet, nous ne souhaitons pas avoir cette impression d’incliner la tête.
La petite astuce évoquée va permettre de traiter ce point sans entrer dans des calculs plus complexes de décomposition de la valeur h en deux rotations, une sur l’axe X et l’autre sur l’axe Z.
L’astuce consiste à placer deux TDummy (rubrique « Scène 3D »), l’un en tant qu’enfant de l’autre. Nous appliquerons la rotation de valeur l autour de l’axe Y du TDummy parent et la rotation de valeur h autour de l’axe X du TDummy enfant.
Pour bénéficier de la composition des deux rotations, la caméra sera placée en tant qu’enfant du second TDummy.
Revenons sous Delphi et implémentons ce que nous venons de voir.
Commençons par placer deux TDummy de la manière suivante :
- Pour le premier TDummy, nous le plaçons en tant qu’enfant du dmyMonde et nous lui affectons les propriétés suivantes via l’inspecteur d’objets :
- Le second TDummy est enfant de dmyJoueurOrientation, et nous lui affectons la propriété suivante :
- Name à dmyJoueurOrientation ;
- Position.Y à -30.
- Name à dmyJoueur.
Ensuite, via la vue structure, déplaçons Camera1 afin de la rendre enfant de dmyJoueur. À l’aide de l’inspecteur d’objets, modifions sa propriété Position.Z pour lui affecter la valeur 0. Au démarrage, la position de l’utilisateur ne sera plus éloignée de l’île, mais au milieu et au-dessus : c’est la position du dmyJoueurOrientation qui fait maintenant office de position de l’utilisateur.
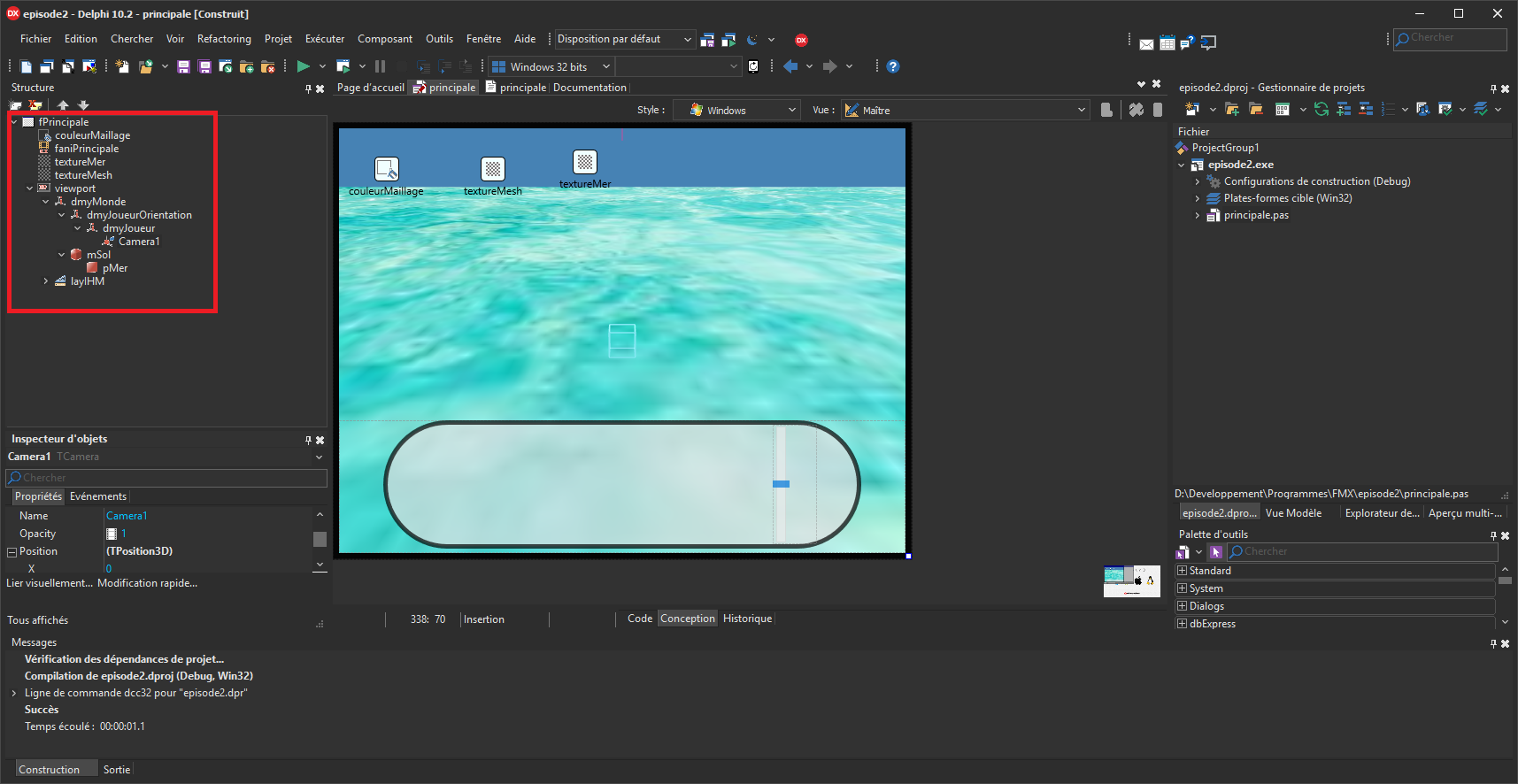
Voici ce que vous devriez avoir sous Delphi :
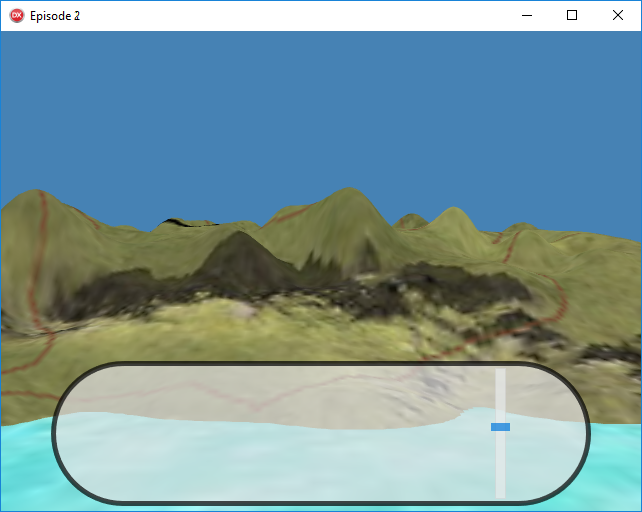
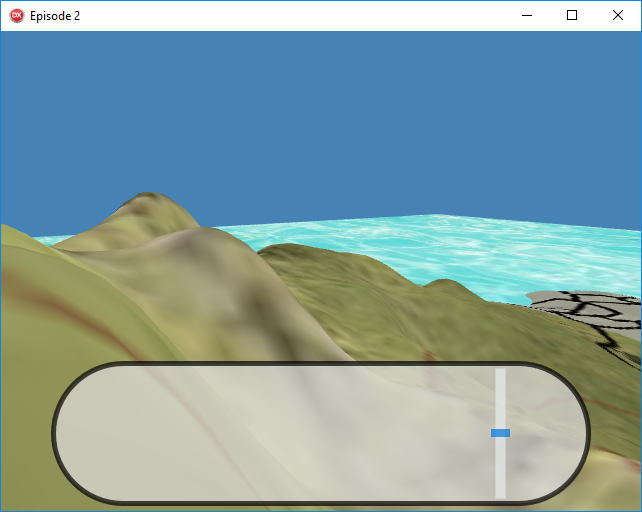
En exécutant le projet, nous constatons que la position du point de vue a effectivement changé :
D’un point de vue théorique et interface, tout est prêt. Passons maintenant au codage proprement dit.
III-B. Mise en pratique▲
Ajoutons à la classe TfPrincipale des attributs et méthodes qui vont nous servir, avec dans les déclarations privées comme suit :
private
{ Déclarations privées }
FPosDepartCurseur: TPointF; // Position du pointeur de souris au début du mouvement de la souris
procedure SetAngleDeVue(const Value: TPointF); // Modification de l'angle de vue
function GetDirection: TPoint3D; // Direction du mouvementComplétons les déclarations publiques avec le code suivant :
property posDepartCurseur: TPointF read FPosDepartCurseur write FPosDepartCurseur; // Propriété de la position du pointeur de souris au début du mouvement de la souris
property angleDeVue : TPointF write SetAngleDeVue; // Propriété de l'angle de vue
property direction : TPoint3D read GetDirection; // Propriété de la directionNous avons vu que la première chose à faire pour gérer l’orientation est de récupérer les coordonnées du pointeur de la souris lorsque l’utilisateur clique sur le Viewport. La propriété posDepartCurseur que nous venons d'ajouter à fPrincipale va permettre de récupérer le point de départ du mouvement de la souris (le point A sur les illustrations précédentes).
Sélectionnons le Viewport, générons son événement OnMouseDown et plaçons-y le code suivant :
procedure TfPrincipale.viewportMouseDown(Sender: TObject; Button: TMouseButton;
Shift: TShiftState; X, Y: Single);
begin
if ssLeft in shift then posDepartCurseur := PointF(X,Y);
end;Rien de compliqué dans ce code : si l’utilisateur a cliqué avec le bouton gauche, nous initialisons posDepartCurseur avec les coordonnées du pointeur de la souris.
Gérons maintenant le déplacement de la souris tout en maintenant le bouton gauche de la souris enfoncé. Pour ce faire, toujours à partir du Viewport, générons son événement OnMouseMove avec le code suivant :
procedure TfPrincipale.viewportMouseMove(Sender: TObject; Shift: TShiftState; X, Y: Single);
begin
if ssLeft in shift then angleDeVue := PointF(X,Y);
end;Le code est simple : si le bouton gauche est enfoncé, nous renseignons la propriété angleDeVue avec la nouvelle position du pointeur de souris.
Le fait de modifier la valeur de la propriété angleDeVue va automatiquement déclencher l’exécution de la méthode SetAngleVue.
Passons donc à la méthode SetAngleDeVue. Cette méthode va implémenter ce que nous avons vu dans le paragraphe III-A :
procedure TfPrincipale.SetAngleDeVue(const Value: TPointF);
var
ptA,ptD,S : TPointF; // ptA point d'arrivée, ptD point de départ, S la sensibilité
begin
S.X := 180 / Viewport.Width; // Réglage de la sensibilité pour l'orientation droite/gauche
S.Y := 180 / Viewport.Height;// Réglage de la sensibilité pour l'orientation haut/bas
ptA := Value * S; // Point d'arrivée adapté à la sensibilité
ptD := posDepartCurseur * S; // Point de départ adapté à la sensibilité
// Vue droite/gauche
with dmyJoueurOrientation.RotationAngle do y:= y + (ptA.X - ptD.X); // orientation droite/gauche (axe y) en fonction du déplacement de la souris en X
// Vue Haut/Bas
with dmyJoueur.RotationAngle do x:= x + (ptD.Y - ptA.Y); // de même pour l'orientation haut/bas en adaptant (rotation sur l'axe x, en fonction du déplacement de la souris en Y
posDepartCurseur := Value; // la position du curseur lorsque l'utilisateur a cliqué (l'origine de la direction), est mis à jour avec la nouvelle position du curseur : au prochain appel de OnMouseMove, la position de départ doit être la position d'arrivée du coup précédent
end;Exécutons à présent le programme.
Vous pouvez constater qu’en cliquant sur le Viewport, l’orientation du point de vue suit bien les mouvements de la souris. Ne jouez pas encore avec le tbVitesse, car nous avons déplacé la caméra et maintenant ce n’est plus elle qui symbolise la position du joueur mais le dmyJoueurOrientation. En effet, dans le paragraphe II de ce tutoriel, nous avons utilisé la propriété Position.Z de la caméra pour gérer le déplacement.
Nous allons modifier cela pour :
- remplacer l’utilisation de la propriété Position.Z de la caméra par la position du dmyJoueurOrientation ;
- utiliser la direction pour partir dans la bonne direction.
Par rapport au paragraphe II, remplaçons le contenu de la procédure faniPrincipaleProcess par celui-ci :
procedure TfPrincipale.faniPrincipaleProcess(Sender: TObject);
var
P: TPoint3D; // Point en 3D qui sera la position du joueur
begin
P := dmyJoueurOrientation.Position.Point + direction * tbVitesse.value;
dmyJoueurOrientation.Position.Point:=P;
end;La variable P va nous permettre de calculer les nouvelles coordonnées de la position du joueur. La nouvelle position du joueur sera l’ancienne position augmentée du déplacement, c’est-à-dire la combinaison de la direction et de la vitesse.
Cette combinaison se calcule en faisant le produit de la direction (propriété de type TPoint3D que nous avons ajoutée à fPrincipale) et de la valeur du tbVitesse.
Le fait de multiplier la direction par la valeur du tbVitesse permet en une opération de multiplier les valeurs des trois coordonnées du TPoint3D (X, Y et Z).
Enfin, nous affectons la nouvelle position du joueur calculée à dmyJoueurOrientation.
Il nous reste à voir le code de la fonction GetDirection qui sera invoquée automatiquement dès que nous souhaiterons accéder à la propriété direction de fPrincipale.
function TfPrincipale.GetDirection: TPoint3D;
begin
result := Point3D(1,0,1) * (Camera1.AbsolutePosition - dmyJoueurOrientation.AbsolutePosition).Normalize; // Détermination de l'orientation
end;Nous normalisons le vecteur entre la caméra et la position du joueur et nous le multiplions par un TPoint3D de coordonnées X = 1, Y = 0 et Z = 1.
Pourquoi ? Dans le projet FMX Island, nous considérons que le joueur est un piéton ou qu’il est en voiture : il est posé au sol. Ses déplacements seront contraints et il ne se déplacera que sur les axes X et Z. L’axe Y devra évoluer automatiquement (quelle que soit l’orientation) en fonction des aspérités du terrain.
Si nous souhaitons faire un simulateur de vol par exemple, et ainsi autoriser un déplacement sur les trois axes, il faudra remplacer Point3D(1,0,1) par Point3D(1,1,1) dans la multiplication.
Exécutez le projet et cette fois-ci, vous constaterez que vous êtes libre de vos déplacements.
IV. Conclusion de cet épisode et la suite▲
Ce second épisode nous a permis d’apprendre à nous orienter et nous déplacer librement dans notre petit monde virtuel en 3D. Je vous donne rendez-vous dans le prochain épisode dans lequel nous agrémenterons de diverses manières ce petit monde 3D.
Vous pouvez retrouver les sources de cet épisode 2 : https://gbegreg.developpez.com/tutoriels/delphi/firemonkey/FMXIsland/episode2/src/episode2_src.zip
V. Remerciements▲
Je vous remercie d’avoir suivi cet épisode. J’espère qu’il vous a plu.
Merci aux relecteurs et correcteurs de ce tutoriel : SergioMaster, GVasseur58 et f-leb.
Enfin, je remercie l'équipe de Developpez.com pour son travail et son soutien.